Introduction

The 8-puzzle is a classic problem in AI and computer science, involving a 3x3 grid where tiles numbered 1 through 8 must be rearranged into a specific goal configuration. The challenge lies in finding the shortest sequence of moves to achieve this goal, often requiring heuristic search algorithms. This page provides a detailed breakdown of the solution implemented in Python.

Code Breakdown

The code is divided into several classes that model the different components of the 8-puzzle problem:


Sq8Action Class: This class models an action in the 8-puzzle, such as sliding a tile from one position to another. It inherits from a base `Action` class and adds details specific to the 8-puzzle, like the tile being moved and its source and destination positions.


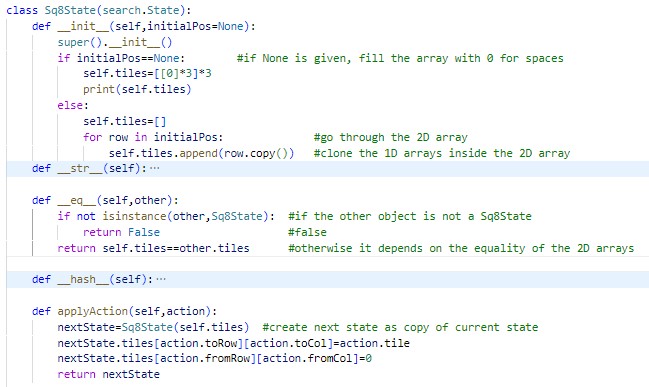
Sq8State Class: The `Sq8State` class represents the state of the puzzle at any given time. It includes methods for displaying the state, comparing states, generating successors (i.e., possible moves), and applying actions. For instance, the `__str__` method converts the state into a human-readable string format, showing tiles and empty spaces.


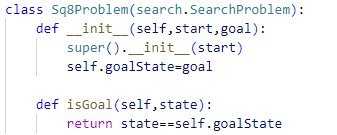
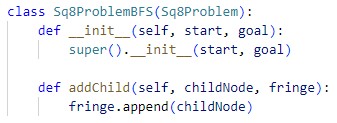
Sq8Problem Class: This class models the overall 8-puzzle problem, integrating the initial state, goal state, and the logic to determine whether a state is the goal. It can be used with search algorithms like BFS or DFS to find the solution.


Code Samples

Sq8Action Class

This class models an action in the 8-puzzle game. It represents the movement of a tile from one position to another on the board. The cost of each action is set to 1.0, which is inherited from the `Action` class.

qsolution

The `__init__` method initializes the action with the tile being moved and its original and new positions. The `__str__` method provides a string representation of the action for easy visualization.


Key Parts of the Sq8State Class

The `Sq8State` class represents the state of the 8-puzzle board. Below are key methods that handle state initialization, comparison, and action application.

qsolution
  • Initialization (`__init__`): Sets up the initial board state based on a 2D array or fills it with zeros if no array is provided.
  • Equality Check (`__eq__`): Compares two states to see if they are identical, based on the arrangement of tiles.
  • Apply Action (`applyAction`): Transforms the current state by applying a given action, resulting in a new state.

Sq8Problem Class

This class defines the 8-puzzle problem and provides methods to check if a given state is the goal state. It serves as a foundation for both BFS and DFS implementations.

qsolution

The Sq8Problem class is initialized with a start state and a goal state. The `isGoal` method checks whether a given state matches the goal state, which is used to determine if the puzzle is solved.


Sq8ProblemDFS Class

This class extends Sq8Problem to implement Depth-First Search (DFS). It overrides the `addChild` method to insert child nodes at the beginning of the fringe, ensuring DFS traversal order.

qsolution

The Sq8ProblemDFS class modifies the `addChild` method to follow DFS by inserting new nodes at the front of the fringe (a list used as the stack for DFS).


Sq8ProblemBFS Class

This class extends Sq8Problem to implement Breadth-First Search (BFS). It overrides the `addChild` method to append child nodes to the end of the fringe, ensuring BFS traversal order.

qsolution

The Sq8ProblemBFS class modifies the `addChild` method to follow BFS by appending new nodes to the back of the fringe (a list used as the queue for BFS).


Solution Visualization

Below is an example of the printed output illustrating how the solution is presented:

8solution

Conclusion

The 8-puzzle problem serves as a fundamental exercise in AI, illustrating the principles of state-space search and the challenges of heuristic problem-solving. Through the use of classes like `Sq8Action`, `Sq8State`, and `Sq8Problem`, we've demonstrated how to model complex problems in a structured and modular way. Whether using BFS, DFS, or other search strategies, the implementation showcases how AI can effectively navigate and solve puzzles that require logical and systematic thinking.


This project not only highlights the power of search algorithms in AI but also emphasizes the importance of problem modeling, efficient state management, and clear action definitions. These concepts are essential in various AI applications beyond puzzles, including robotics, game development, and automated decision-making systems.


Full Code Dog Walking Problem Queen Problem