Introduction

The N-Queen problem is a classic example in AI, representing a challenge where N queens must be placed on an N×N chessboard so that no two queens threaten each other. Various AI techniques such as hill-climbing, simulated annealing, and sideway moves are employed to solve this problem efficiently.

Code Breakdown

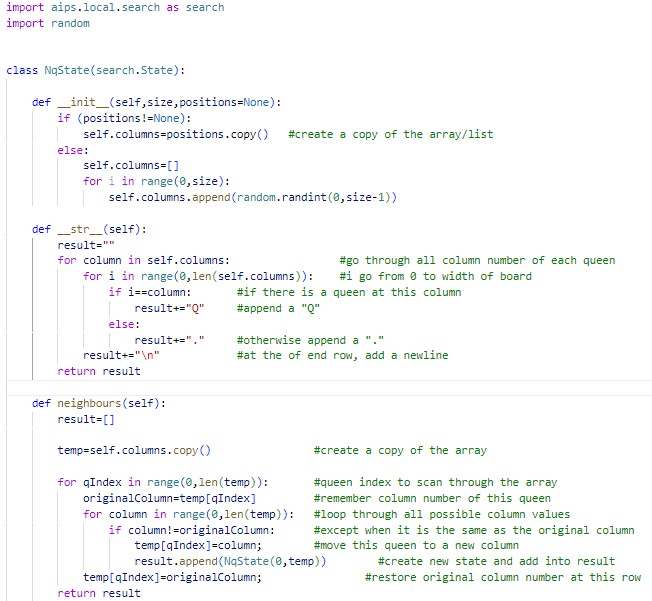
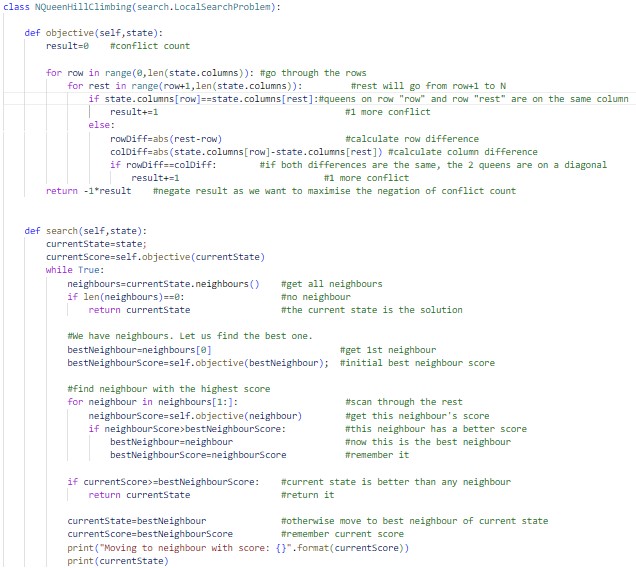
The code is structured around object-oriented principles with classes modeling the problem and its solutions. The NqState class represents the state of the N-Queen problem, storing the positions of the queens. The NQueenHillClimbing, NQueenSidewayMove, and NQueenSimulatedAnnealing classes implement different strategies to find the solution.


  • NqState: Manages the positions of queens and generates neighboring states.

  • NQueenHillClimbing: Implements the hill-climbing algorithm to maximize the negation of conflicts between queens.

  • NQueenSidewayMove: Extends hill-climbing to include sideway moves, allowing movement across flat landscapes.

  • NQueenSimulatedAnnealing: Uses simulated annealing to avoid local maxima by probabilistically accepting worse states.


Code Samples

NqState Class

This class models the state of the N-Queen problem. It represents the positions of the queens on the board and provides methods to visualize the board and generate neighboring states.

nqstate

The __init__ method initializes the state with either a provided list of positions or random positions. The __str__ method generates a visual representation of the board, and the neighbours method produces all possible states resulting from moving a single queen to a new position.


NQueenHillClimbing Class

This class implements the hill-climbing search algorithm for solving the N-Queen problem. It evaluates states based on the number of conflicting queens and attempts to find an optimal solution by iteratively moving to better neighboring states.

nqueenhillclimbing

The objective method calculates the number of conflicting queen pairs, aiming to minimize this number. The search method performs the hill-climbing algorithm, seeking to maximize the objective function (i.e., minimize conflicts). It continues to iterate until no better neighboring state is found.


Solution Visualization

Below is an example of the printed output illustrating how the solution is presented:

qsolution

Conclusion

The N-Queen problem illustrates the power of AI in solving combinatorial problems. By using different approaches like hill-climbing and simulated annealing, we can efficiently find solutions even in complex scenarios. Each method has its strengths: hill-climbing is quick but prone to getting stuck in local maxima, while simulated annealing provides a robust solution by allowing exploration of worse states.

Full Code Dog Walking Problem 8 Square